eWEEK content material and product suggestions are editorially unbiased. We could earn a living if you click on on hyperlinks to our companions. Learn More.
Linear regression often is the most simple and accessible machine studying (ML) algorithm, nevertheless it’s additionally one of many quickest and strongest. As a end result, professionals in enterprise, science, and academia incessantly depend on this broadly used methodology for predictive evaluation. Understanding how linear regression works, its sorts and attributes, its key advantages, and its fundamental functions throughout varied fields may help you take advantage of it in your online business.
KEY TAKEAWAYS
- •Three varieties of linear regression embrace easy (single), a number of, and polynomial regression. (Jump to Section)
- •Linear regression is used throughout varied fields, from enterprise and economics to healthcare and the social sciences. (Jump to Section)
- •Effective strategies can be found to handle the frequent challenges of utilizing linear regression fashions. (Jump to Section)
What Is Linear Regression and How Does it Work?
At essentially the most fundamental stage, linear regression depends on one variable—the unbiased variable—to foretell the worth of one other variable: the dependent variable. This simple components for making correct predictions allows extremely explainable synthetic intelligence (XAI) that may be skilled shortly.
It originated within the improvement of statistical strategies for analyzing human measurements pioneered by Victorian-era naturalist and behavioral geneticist Sir Francis Galton. In learning the relative heights of fathers and sons, Galton noticed that offspring tended to deviate much less from the inhabitants’s imply top worth when in comparison with their dad and mom, whilst taller-than-average fathers usually produced taller-than-average sons.
This statistical phenomenon—the “regression to the mean”—dictates that when a random variable’s pattern worth is excessive, subsequent samples of the identical random variable will fall near the inhabitants’s imply.
How Linear Regression Works
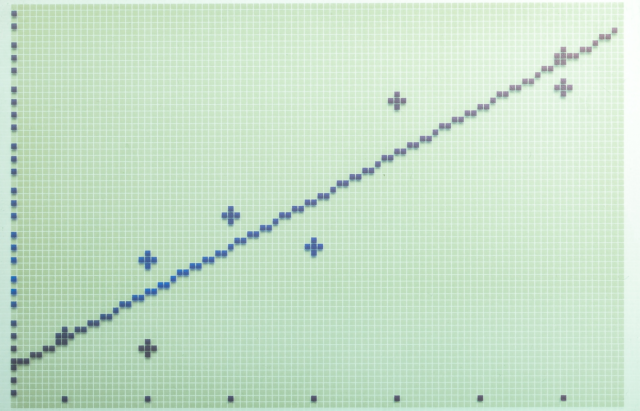
Linear regression works on the idea that when excessive outcomes are noticed in random information samples, extra regular information factors are prone to observe—and {that a} straight line can match between the plotted information factors. This line can be utilized as a reference for minimizing predicted and precise output worth discrepancies. Further, statistical strategies will be derived from regression evaluation to estimate relationships between dependent variables and a number of unbiased variables.
The regression to the imply phenomenon applies to nearly any measurable parent-offspring attribute. Statisticians acknowledge it as a mathematical reality of pure variation in repeated information and depend on this premise to reduce sudden variations in predicted and precise output values.
Independent and Dependent Variables in Linear Regression
In regression evaluation, the end result variable is the dependent variable, and the confounding variable is the predictor or unbiased variable. In less complicated phrases, the unbiased variable X is the trigger, and the dependent variable Y is the impact. For instance, the noticed information in Galton’s analysis appeared to indicate an affiliation between two variables—a father’s top and his son’s top—so a tall father’s top (X) could be typically anticipated to lead to a tall son’s top (Y).
In a linear regression plot, the straight line represents the perfect try to reduce the residual sum of squares between recognized or noticed information factors and the anticipated information factors. For this purpose, the regression line can also be known as a best-fit line, and the strategy used for this becoming method is known as the least…
